Réciproque du théorème de Thales
Dans un triangle quelconque, un segment joint deux points des deux côtes du triangle. Si on peut écrire l’égalité des deux rapports concernant les segments sur les deux côtés, le segment qui joint les deux points est parallèle à la base.
Le triangle est ABC, les points sur les côtés sont P et Q, les segments sont respectivement a,b,c,d selon la figure ci-dessous :
Les rapports sont (relation (1)) : a/b=c/d
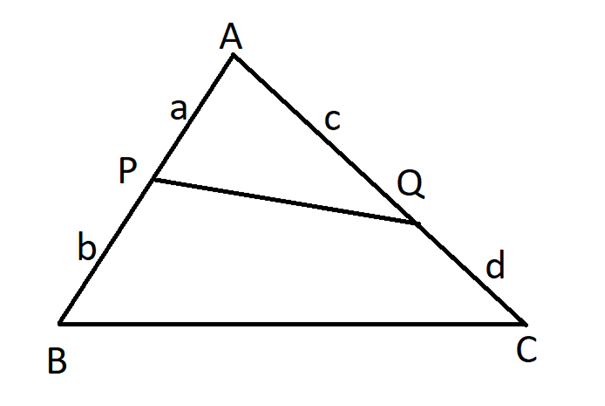
Le théorème affirme que si l’égalité (1) est vérifiée, le segment PQ est parallèle à BC
Pour la démonstration il faut faire appel à un lemme (démonstration simple préliminaire):
LEMME :
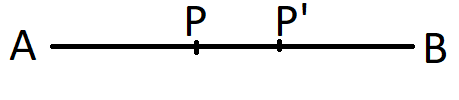
Quand un point partage un segment de droite, le rapport entre les segments naissants est unique (appelé le rapport de section).
Soit P le point initial et supposons qu’il puisse exister un deuxième point P’ tel que AP/PB=AP’/P’B=k (2)
Notons que AP+PB=AB (3) et que AP’+P’B=AB aussi (4)
D’après (2) AP=k.PB et AP’=k.P’B
Remplaçant dans (3) et (4) on obtient :
((k+1).PB = (k+1).P’B=AB en simplifiant par k+1toujours différent de zéro, il vient que PB=P’B
Donc le point P est le seul qui partage le segment AB dans le rapport de section k
En réalité en géométrie orientée, on trouve qu’il existe un point externe au segment AB, sur le même alignement mais le rapport vaut –k.
Maintenant on peut attaquer la démonstration de la réciproque du théorème de THALES
Nous devons d’abord faire appel à un artifice de calcul c’est-à-dire à une astuce qui permet de réaliser la démonstration.
Dans le Triangle ABC nous avons la relation AP/PB=AQ/QC=k (rapport de section de AB et AC.
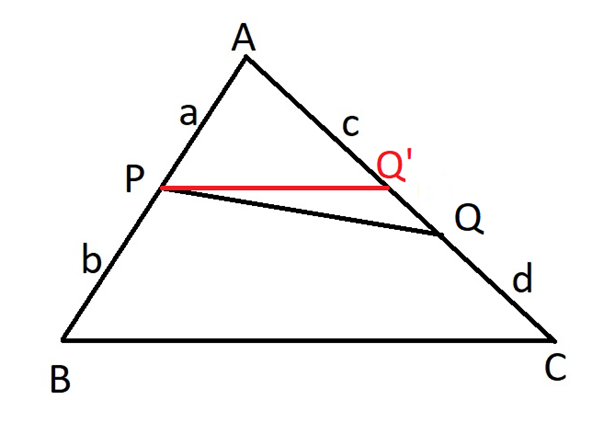
Par P construisons une parallèle à la base qui coupe la droite AC en Q’.
Par Thales nous avons AP/PB=AQ’/Q’C=k
Donc le point Q’ et Q ont le même rapport de section par rapport au segment de droite AC. Donc ces deux points sont confondus en vertu du lemme et PQ est obligatoirement parallèle à la base. CQFD
Dr. STRUL Salomon
Neuropsychiatre