Les troubles de la phonation
Dr. STRUL Salomon
Nous tenons à préciser naturellement qu’il s’agit des troubles de la phonation chez l’homme donc de troubles liés au fonctionnement des cordes vocales.
Mais les mêmes problèmes peuvent se poser chez tous les animaux dont les sons émis dépendent de cordes vibrantes.
Notre métier d’ingénieur mécanicien nous a conduit à étudier les phénomènes liés à l’acoustique, c’est-à-dire liés à la propagation du son dans les divers milieux.
Nous avons rencontrés sans entrer dans le détail des démonstrations qui relèvent de la physique mathématique, une formule qui fournit la fréquence de vibration de cordes fixées aux deux extrémités.
Nous tenons à préciser qu’une corde en mécanique est le nom donné à une barre soumise à une force de traction axiale importante. Soit T le grandeur de la force de traction axiale en Newtons.
Une corde possède encore une autre série de propriétés que nous allons énumérer.
En premier lieu une corde a une longueur (l) qui est la même que la distance entre les deux points de fixation de cette corde, en mètres.
Une corde à une section transversale dont la forme peut varier mais ce qui nous intéresse c’est la superficie de cette section (S) en mètres ².
Une corde est constituée d’un matériau spécifique ou d’un alliage mais il a une masse spécifique (ϱ) exprimée en kg/m³.
De plus, une corde peut, pour une même longueur, vibrer à un multiple entier (n) de la fréquence de base dont la demi-longueur d’onde vaut justement la longueur de la corde puisque la forme de la corde en cours de vibration est sinusoïdale.
Tout ceci est résumé par la formule suivante dite « des cordes vibrantes » :
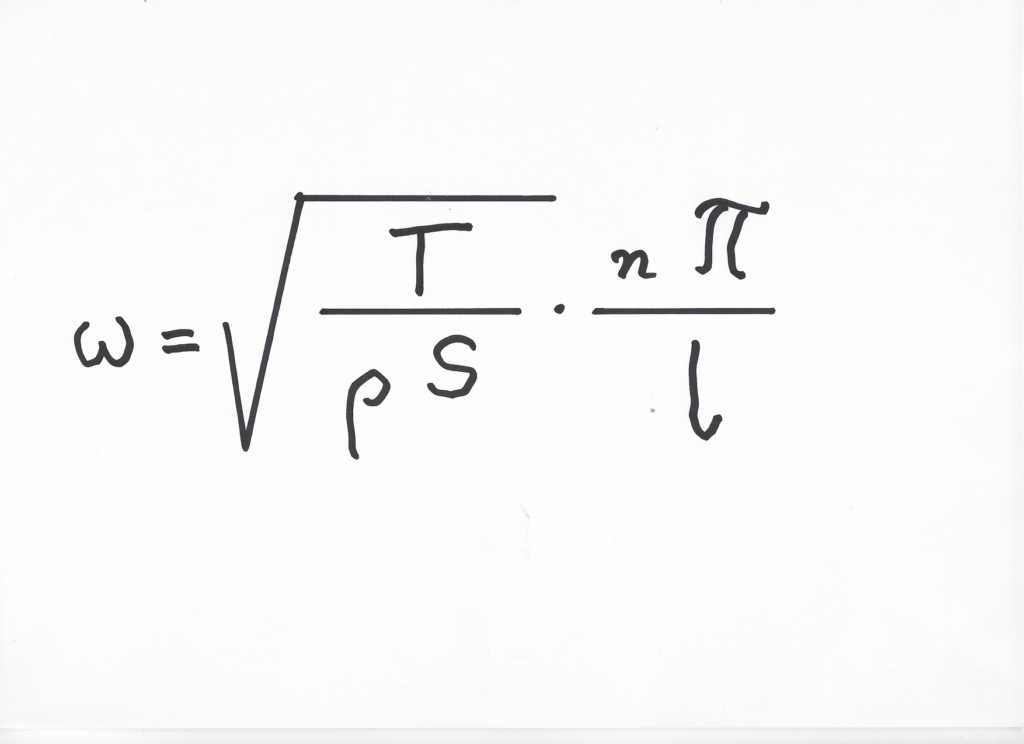
Le terme de gauche ω représente la pulsation c’est-à-dire l’angle en radians effectué par unité de temps et est lié à la fréquence de vibration par la relation simple :
ω = 2 π ν
ν est la fréquence en cycles par sec. ou Hertz (Hz):
Nous allons reprendre chaque paramètre de la formule et le relier à une pathologie spécifique du système de phonation.
- Paramètre T ou tension axiale qui règne dans la corde vocale (en Newtons) est crée par les muscles aryténoïdes qui dépendent du Nerf Récurrent, lui-même branche du nerf vague. En fait c’est le facteur le plus important dans l’élaboration de la parole puisqu’il règle la hauteur du son émis par les cordes vocales, c’est à dire de la VOIX !
Dans les maladies neuromusculaires cette tension fluctue et baisse ou devient absente produisant la paralysie de la corde vocale. La voix devient « bitonale » c’est-à-dire instable comme celle d’une trompète dont on souffle mal et on n’arrive pas à garder une note unique.
La myasthénie affaiblit les muscles aryténoïdes et la voix devient évanescente. Les compressions du nerf récurant par des métastases de cancers pulmonaires produisent la voix bitonale.
2. Paramètre ϱ ou masse spécifique (en kg/m³). Ce facteur dépend du tissu dans lequel est constitué la corde vocale est il est en général conjonctif, fibroblastique. Il peut se modifier en cas d’œdème, c’est-à-dire d’infiltration d’eau et s’alourdir. La voix devient donc rauque comme dans les laryngites, chez les tabagiques, alcooliques… Les nodules sur les cordes vocales interviennent dans le même paramètre et rendent la voix plus rauque (grave).
3. Le paramètre S donne la surface (en m²) de la section de la corde vocale. La voix de l’enfant est plus aigue que celle de l’adulte puisque S augmente avec la croissance. De même l’œdème et les infiltrats pathologiques augmentent le facteur S
4. Le facteur l ou longueur de la corde (en mètres) est plus grand chez l’homme et plus court chez la femme et l’enfant. Donc la voix masculine est plus grave que la voix féminine ou enfantine.
Enfin le facteur n permet avec une même corde vocale de produire par exemple une note DO d’une fréquence donnée, la note une octave au dessus et avec une peu d’entrainement on peut couvrir plusieurs octaves de la sorte.
Le terme π est là pour transformer les battements par seconde en angles mesurés en radians.
Voici donc comment on peut résumer un ensemble de pathologies ou de disfonctionnements du système de phonation, grâce à une formule mathématique simple et facile à retenir comme moyen mnémotechnique.