Théorème de projectivité de STRUL (dual de PASCAL)
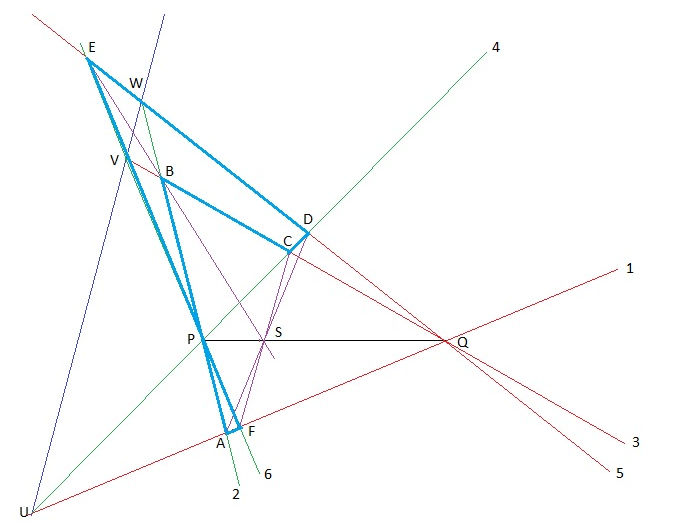
Soient dans un plan deux points définissant une droite PQ.
Soient 3 droites quelconque concurrentes en P (nommées 2,6,4)
Soient 3 droites quelconques concurrentes en Q (nommées 1,3,5)
Ces 6 droites constituent le côté d’une hexagone irrégulier, convexe dont les sommets sont ABCDEF
En joignant les sommets opposés on obtient 3 droites, AD, BE et CF qui sont concurrentes en un point nommé S.
Si par hasard, les cotés opposés (1,4), (2,5) et (3,6) se coupent en trois points colinéaires, (en U,V,W) le point S se trouve sur la droite initiale PQ.
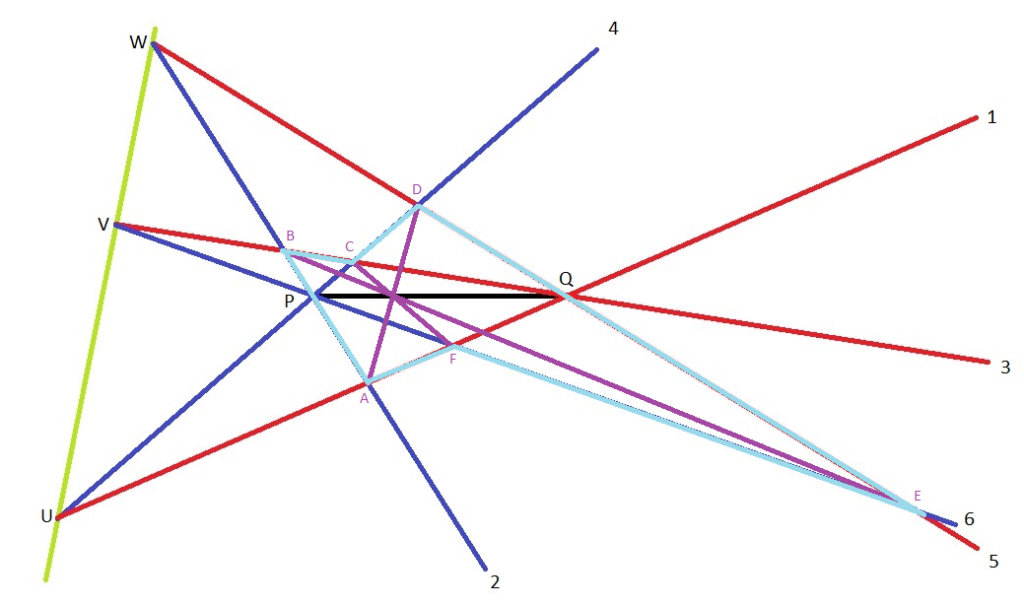
Le théorème de Pascal s’applique à toutes les coniques et le cas particulier de projectivité s’applique à deux droites soit une conique dégénérée.
Mon théorème s’applique à deux points soit le dual de la conique dégénérée en deux droites.
Mon théorème ne nécessite aucune démonstration vu que son dual, a été démontré par Pascal à l’aide des birapports.
Le théorème de Pascal considère deux droites et leur point d’intersection comme une conique dégénéré. Je considère deux points et la droite qui les rejoints comme une conique dégénérée