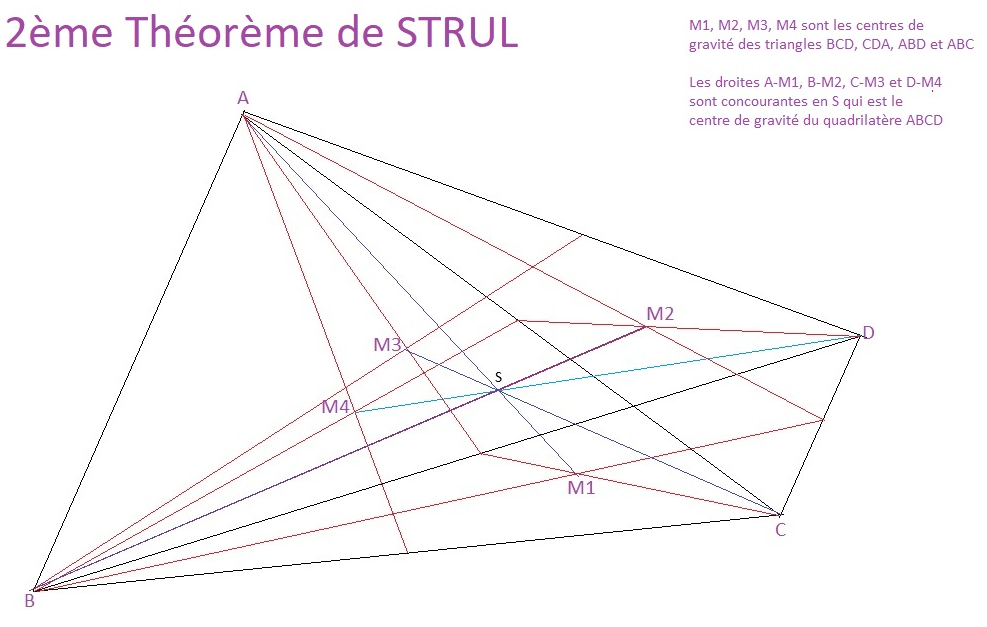
2ème théorème de STRUL
Dans un quadrilatère quelconque les quatre droites qui joignent les sommets successifs aux centres de gravité des triangles restants sont concourantes.
Soit le quadrilatère quelconque ABCD. Si on choisit le sommet A, le tringle restant est BCD. Si on choisit le sommet B, le triangle restant est CDA et ainsi de suite.
Ce théorème est une évidence puisqu’il s’agit de la projection plane d’un tétraèdre et des droites joignant les divers sommets aux centres de gravités des triangles opposés aux sommets choisis. Il s’agit en fait du centre de gravité du tétraèdre et les 4 médianes sont concourantes dans l’espace. La concourance est une propriété projective. D’où évidence du théorème en question.