THEOREME de la BISSECTRICE dans un triangle et sa RECIPROQUE
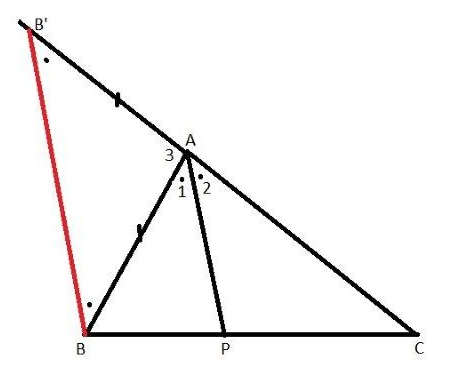
Soit un triangle quelconque ABC et soit AP la bissectrice issue de A, angle intérieur du triangle.
Soient A1 et A2, les angles crées par la bissectrice qui sont égaux par définition.
Prolongeons le côté AC au delà de A.
A l’aide d’un compas, reportons la longueur du coté AB sur le prolongement de AC à l’extérieur du triangle comme sur la figure. On obtient le point B’. Joignons B à B’. On obtient BB’ en rouge
Comme AB=AB’, le triangle ABB’ est isocèle. Donc les angles B et B’ marqués d’un point sont égaux.
Dans le triangle ABB’ la somme des angles vaut 180° comme dans tous les triangles plans.
Mais le long de la droite CB’ l’angle A vaut aussi 180° car ligne droite ! On a nomme A3 l’angle du sommet A du triangle ABB’.
On peut écrire :
A3+B+B’=180° mais A3+A1+A2=180°. Or A1=A2. Donc les angles B=B’=A1=A2
Et les droites B’B et AP sont parallèles car des angles alternes internes B’ et A1 sont égaux.
Donc on peut appliquer THALES et écrire l’égalité des rapports suivante :
AB’/AC=PB/PC mais AB’=AB
DONC en finale théorème de la bissectrice : AB/AC=PB/PC et en français :
La bissectrice partage le côté opposé à son angle dans le même rapport que celui des deux côtés adjacents.
RECIPROQUE DU THEOREME DE LA BISSECTRICE
Si une droite issue d’un sommet d’un triangle partage le côté opposé dans le même rapport de section que les côtés adjacents, alors cette droite est bissectrice de l’angle en question.
On refait la même construction que pour le théorème direct mais on ne sait pas si la droite AP et la bissectrice de l’angle A intérieur au triangle.
Données de base (hypothèse) : Le rapport AB/AC=BP/PC
Mais comme AB’=AB par construction, on peut écrire le rapport B’A/AC=BP/PC et selon la réciproque du théorème de THALES, AP est parallèle à B’B. Donc l’angle B’=angle A2 comme angles correspondants de deux droites parallèles et l’angle A1= l’angle B comme alternes internes de deux droites parallèles. Mais le triangle ABB’ est isocèle par construction. Donc l’angle A1= angle A2 et la droite AP est la bissectrice de l’angle A. CQFD